Hello friends today’s topic is Geometry. In Geometry we will learn what is Geometry.
We will also see some Geometrical proofs. I think there are many students that always struggle in Geometrical proofs. So today I’ll try to explain it to you using examples and diagrams.
As a Grade IX student you should first know what is Geometry?
Geometry is every where around us whether it is man made thing, nature, arts, sports etc.
Geometry is basically about shapes and sizes based upon four imaginary ideas- point, line, plane and space.
Geometrical proofs illustrate step by step conclusion of a geometric statement using definitions, postulates, axioms and previously proved theorems.
There are two major types of proofs:
Direct Proof is based on deductive reasoning in which the conclusion is made directly from the previous conclusions.
Indirect Proof includes the negative assumption of the statement our end result leads to contradiction which states that the inverse of assumed statement is true.
Geometrical proofs can be written either in two columns or in paragraph.
In two columns geometrical proofs we have two columns one consists of list of statements and other consists of the reasons which states why the statement is true.
Paragraph proof is only the two column proof written in paragraph.
Example 1:

Given: DEFG is a parallelogram.
Proof: angle G and E are congruent.
Solution:
Example 2:
Proof that area of a circle is pi*r2 .
Solution:
Here we prove that area of a Circle ( A ) is pi * r2.
A = pi * r2
We will proof this by using some images as it is easy to understand.

Do you find any difference in both the images? No ! Look the area outside the circle but inside the square reduced as we move from 4 side square to 8 side octagon.
Now if we increase the number of sides, the space will become very small.
Keeping that statement in mind let’s look at the following image:
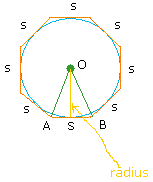
from the image above area of triangle AOB is :
AOB = ½(base * height) = ½(s*r)
Where r = radius
As outer shape is octagon so we can create 8 triangles inside it. As the image below:
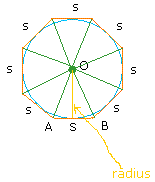
Now the area of octagon is:
8* (1/2 (s*r ) ) = 1/2r * 8s
8s is the perimeter of octagon.
And as we have stated before that as we increase the number of sides to n resulting in n-gon will look like exactly same as circle. So that the perimeter of the octagon is almost same as the perimeter of circle.
Hence we can replace the 8s by 2 x pi x r.
Which is the perimeter of the circle. For calculating area of circle the number of side is very large.
By doing it (increasing the no of sides), the area of circle will be:
1/2 r * 2 * pi * r = pi * r2
Remember this is what we are trying to prove.
So The Area of circle is = pi * r2.
We will also see some Geometrical proofs. I think there are many students that always struggle in Geometrical proofs. So today I’ll try to explain it to you using examples and diagrams.
As a Grade IX student you should first know what is Geometry?
Geometry is every where around us whether it is man made thing, nature, arts, sports etc.
Geometry is basically about shapes and sizes based upon four imaginary ideas- point, line, plane and space.
Geometrical proofs illustrate step by step conclusion of a geometric statement using definitions, postulates, axioms and previously proved theorems.
There are two major types of proofs:
Direct Proof is based on deductive reasoning in which the conclusion is made directly from the previous conclusions.
Indirect Proof includes the negative assumption of the statement our end result leads to contradiction which states that the inverse of assumed statement is true.
Geometrical proofs can be written either in two columns or in paragraph.
In two columns geometrical proofs we have two columns one consists of list of statements and other consists of the reasons which states why the statement is true.
| Statements | Reason |
Paragraph proof is only the two column proof written in paragraph.
Example 1:

Given: DEFG is a parallelogram.
Proof: angle G and E are congruent.
Solution:
| Statements | Reason |
| 1.DEFG is parallelogram | Given |
| 2.DE parallel to GF | Definition of parallelogram |
| 3.Angle GDF congruent to angle EFD | When transversal cuts parallel line, interior angles are congruent. |
| 4.Angle GFD congruent to angle EDF | When transversal cuts parallel line, interior angles are congruent. |
| 5.Segment DF is congruent to itself | Reflexive proporty |
| 6.Triangle GDF congruent to triangle EFD | From postulate 3, 4, 5 |
| 7.Angle G and E are congruent | Corresponding parts of congruent triangles are congruent. |
Example 2:
Proof that area of a circle is pi*r2 .
Solution:
Here we prove that area of a Circle ( A ) is pi * r2.
A = pi * r2
We will proof this by using some images as it is easy to understand.

Do you find any difference in both the images? No ! Look the area outside the circle but inside the square reduced as we move from 4 side square to 8 side octagon.
Now if we increase the number of sides, the space will become very small.
Keeping that statement in mind let’s look at the following image:
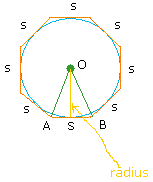
from the image above area of triangle AOB is :
AOB = ½(base * height) = ½(s*r)
Where r = radius
As outer shape is octagon so we can create 8 triangles inside it. As the image below:

Now the area of octagon is:
8* (1/2 (s*r ) ) = 1/2r * 8s
8s is the perimeter of octagon.
And as we have stated before that as we increase the number of sides to n resulting in n-gon will look like exactly same as circle. So that the perimeter of the octagon is almost same as the perimeter of circle.
Hence we can replace the 8s by 2 x pi x r.
Which is the perimeter of the circle. For calculating area of circle the number of side is very large.
By doing it (increasing the no of sides), the area of circle will be:
1/2 r * 2 * pi * r = pi * r2
Remember this is what we are trying to prove.
So The Area of circle is = pi * r2.
No comments:
Post a Comment