Hii guys, we are going to learn about Sequences and Series in our today's session.
A list of numbers when arranged in a proper fashion then the arrangement is called as a sequence. In such a case each member either comes before or after another member. If this arrangement is disturbed then it is no more a sequence.
A series is formed when we do sum of sequence of terms. In a more easy language a series is the list of numbers with the addition operation between them.
For Example -
( a1, a2, a3, … ), or ( b0, b1, b2, … ), or ( c0, c2, c4, … ) are known as sequences and
(a1+ a2 + a3 +....), or (b1 + b2 + b3 + ....), or (c1 + c2 + c3 + …) are known as series.
The sequences are categorized as Finite, Infinite and Multiplicative.
A more formal definition of a finite sequence with terms in a set S is a function from 1, 2, ..., n to S for some n > 0. An infinite sequence in S is a function from 1, 2, ... to S.
The sequence is multiplicative if f( x y) = f(x) f(y) for x and y such that x and y are co prime.
A series is always written with a summation sign in front of it. It is represented as ∑.
For Example -
This is an example of infinite sequence.
And
This one is for an infinite sequence.
There are many types of series, but what we have to learn about is the arithmetic, geometric and Fibonacci series.
Arithmetic series or arithmetic progression is a sequence of numbers such that difference between two consecutive terms always remains constant. It is represented in general as
where an is any number of a sequence.
The sum of this series is given by
![S_n=fracn2[ 2a_1 + (n-1)d].](http://upload.wikimedia.org/wikipedia/en/math/7/4/5/7456a8d727899b701af9e209bed95cdc.png)
where n is the number of terms and d is the common difference between them.
A geometric series is one with constant ratios between its terms.
For example
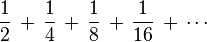
It is represented by:
here a is the first term, r is the common ratio and n is the number of terms.
and the sum of this GP is given by a formula:
s = 1/ (1- r).
where s is the sum and r is the common ratio. But this formula is only for an infinite geometric progression.
The Geometric series is the best example of an infinite series.
Fibonacci series is the series in which each successive term is the addition of the terms preceding it.
The first two terms are 0 and 1, then term next to it is addition of these two.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 and so on.
If you are not able to memorize then you can find them using the formula
Fn = Fn-1+ Fn-2.
A list of numbers when arranged in a proper fashion then the arrangement is called as a sequence. In such a case each member either comes before or after another member. If this arrangement is disturbed then it is no more a sequence.
A series is formed when we do sum of sequence of terms. In a more easy language a series is the list of numbers with the addition operation between them.
For Example -
( a1, a2, a3, … ), or ( b0, b1, b2, … ), or ( c0, c2, c4, … ) are known as sequences and
(a1+ a2 + a3 +....), or (b1 + b2 + b3 + ....), or (c1 + c2 + c3 + …) are known as series.
The sequences are categorized as Finite, Infinite and Multiplicative.
A more formal definition of a finite sequence with terms in a set S is a function from 1, 2, ..., n to S for some n > 0. An infinite sequence in S is a function from 1, 2, ... to S.
The sequence is multiplicative if f( x y) = f(x) f(y) for x and y such that x and y are co prime.
A series is always written with a summation sign in front of it. It is represented as ∑.
For Example -
This is an example of infinite sequence.
And
This one is for an infinite sequence.
There are many types of series, but what we have to learn about is the arithmetic, geometric and Fibonacci series.
Arithmetic series or arithmetic progression is a sequence of numbers such that difference between two consecutive terms always remains constant. It is represented in general as
where an is any number of a sequence.
The sum of this series is given by
where n is the number of terms and d is the common difference between them.
A geometric series is one with constant ratios between its terms.
For example
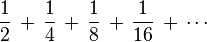
It is represented by:
here a is the first term, r is the common ratio and n is the number of terms.
and the sum of this GP is given by a formula:
s = 1/ (1- r).
where s is the sum and r is the common ratio. But this formula is only for an infinite geometric progression.
The Geometric series is the best example of an infinite series.
Fibonacci series is the series in which each successive term is the addition of the terms preceding it.
The first two terms are 0 and 1, then term next to it is addition of these two.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 and so on.
If you are not able to memorize then you can find them using the formula
Fn = Fn-1+ Fn-2.
No comments:
Post a Comment